导读: 在数学领域中,反函数是一个重要的概念,它能帮助我们从不同角度理解函数关系。maple作为一款强大的数学软件,为我们提供了便捷的求反函数的方法。一、基本原理maple利用其内置的算法和函数库来求解反函数。它会根据给定函数的表达式,通过一系列数学变换和计算,尝试找
在数学领域中,反函数是一个重要的概念,它能帮助我们从不同角度理解函数关系。maple作为一款强大的数学软件,为我们提供了便捷的求反函数的方法。
一、基本原理
maple利用其内置的算法和函数库来求解反函数。它会根据给定函数的表达式,通过一系列数学变换和计算,尝试找到与之对应的反函数表达式。
二、求解步骤
1. 定义函数
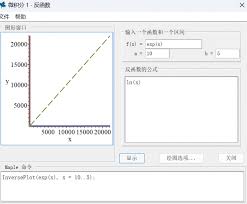
首先,我们需要在maple中定义要求反函数的函数。例如,定义函数⁄(y = 2x + 3⁄),可以输入“f := x -> 2*x + 3;”。
2. 求反函数
然后,使用maple的反函数求解命令。对于上述函数,输入“inverse := solve(y = f(x), x);”,maple会输出⁄(x = ⁄frac{y}{2} - ⁄frac{3}{2}⁄),这就是原函数⁄(y = 2x + 3⁄)的反函数。
三、处理复杂函数
对于一些复杂函数,如三角函数、指数函数等,maple同样能有效地求出反函数。
1. 三角函数反函数

比如求⁄(y = ⁄sin(x)⁄)的反函数。先定义函数“f := x -> sin(x);”,再求反函数“inverse := solve(y = f(x), x);”,maple会输出⁄(x = ⁄arcsin(y)⁄)。
2. 指数函数反函数
定义指数函数“f := x -> 2^x;”,求反函数“inverse := solve(y = f(x), x);”,maple会得到⁄(x = ⁄frac{⁄ln(y)}{⁄ln(2)}⁄),即⁄(x = ⁄log_2(y)⁄)。
四、注意事项
在使用maple求反函数时,要注意原函数的定义域和值域。因为反函数的定义域是原函数的值域,值域是原函数的定义域。如果原函数不是一一对应的,可能无法直接求出单值的反函数。此时,需要对原函数的定义域进行适当限制,使其成为一一对应的函数,然后再求反函数。
通过maple,我们可以轻松地求出各种函数的反函数,这为数学学习、研究和工程应用等提供了极大的便利,帮助我们更深入地探索函数世界的奥秘。
上一篇:美柚如何与苹果手表连接