数学期望值怎么算

在数学的奇妙世界里，数学期望值如同一位神秘的向导，引领我们探索各种随机现象背后的规律。它不仅在概率论中占据着核心地位，在现实生活的众多领域也有着广泛应用。那么，数学期望值究竟该如何计算呢？

一、离散型随机变量的数学期望

对于离散型随机变量 x，其取值为⁄(x_1,x_2,⁄cdots⁄)，对应的概率为⁄(p_1,p_2,⁄cdots⁄)，则数学期望⁄(e(x)=⁄sum_{i}x_ip_i⁄)。

例如，抛一枚均匀的骰子，设随机变量 x 表示骰子的点数。x 的取值为⁄(1,2,3,4,5,6⁄)，且每个点数出现的概率均为⁄(⁄frac{1}{6}⁄)。那么⁄(e(x)=1⁄times⁄frac{1}{6}+2⁄times⁄frac{1}{6}+3⁄times⁄frac{1}{6}+4⁄times⁄frac{1}{6}+5⁄times⁄frac{1}{6}+6⁄times⁄frac{1}{6}=⁄frac{1 + 2 + 3 + 4 + 5 + 6}{6}=⁄frac{21}{6}=3.5⁄)。

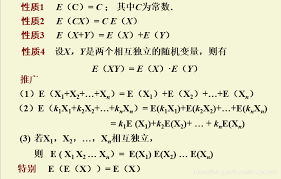
二、连续型随机变量的数学期望

对于连续型随机变量 x，其概率密度函数为⁄(f(x)⁄)，则数学期望⁄(e(x)=⁄int_{-⁄infty}^{⁄infty}xf(x)dx⁄)。

假设某电子产品的使用寿命 x 服从参数为⁄(⁄lambda⁄)的指数分布，其概率密度函数为⁄(f(x)=⁄begin{cases}⁄lambda e^{-⁄lambda x}, & x⁄geq0 ⁄⁄ 0, & x⁄lt0⁄end{cases}⁄)。那么⁄(e(x)=⁄int_{0}^{⁄infty}x⁄lambda e^{-⁄lambda x}dx⁄)，通过分部积分法可得⁄(e(x)=⁄frac{1}{⁄lambda}⁄)。

三、数学期望在实际中的应用

数学期望值在投资决策、风险评估等方面有着重要作用。比如，有一项投资，成功的概率为⁄(0.6⁄)，收益为⁄(100⁄)万元；失败的概率为⁄(0.4⁄)，损失⁄(20⁄)万元。设收益为随机变量 x，则⁄(e(x)=100⁄times0.6 + (-20)⁄times0.4 = 60 - 8 = 52⁄)万元。通过计算数学期望，投资者可以对该投资的平均收益有一个清晰的认识，从而做出更合理的决策。

数学期望值以其独特的魅力，为我们理解和分析随机现象提供了有力的工具，帮助我们在复杂的世界中做出更明智的选择。