Maple微分命令是什么

在数学的浩瀚海洋中，微分是一项至关重要的运算，它帮助我们理解函数的变化率、极值等关键性质。而maple软件为我们提供了强大且便捷的微分命令，让微分运算变得轻松高效，深受广大用户喜爱。

基本微分命令

maple的diff命令是进行微分运算的核心。例如，对于函数$f(x)=x^2$，我们只需在maple中输入diff(x^2,x)，就能迅速得到它的导数$2x$。这个简单的操作，避免了繁琐的手工求导过程，大大节省了时间和精力。无论是多项式函数、三角函数还是指数函数等，diff命令都能准确无误地给出导数结果。

高阶导数计算

不仅如此，maple还能轻松计算高阶导数。若要计算函数$f(x)=sin(x)$的二阶导数，只需输入diff(sin(x),x,x)，就能快速得到$-sin(x)$。对于更复杂的函数，即使是高阶导数的计算，maple也能应对自如。这使得研究函数的高阶变化特性变得轻而易举，为数学分析和物理研究等领域提供了有力支持。

多元函数微分

在处理多元函数时，maple的微分功能同样出色。比如对于二元函数$z = x^2y + y^3$，求关于$x$的偏导数，我们输入diff(x^2*y + y^3,x)，就能得到$2xy$。求关于$y$的偏导数则输入diff(x^2*y + y^3,y)，得到$x^2 + 3y^2$。maple能够清晰地区分不同变量的偏导数计算，让多元函数的微分运算变得有条不紊。

隐函数微分

对于隐函数，maple也有相应的处理方法。假设隐函数方程为$x^2 + y^2 = 25$，我们可以使用maple的隐函数求导功能。通过相关命令，能快速求出$y$关于$x$的导数，这对于研究隐函数的性质和曲线的切线等问题非常有帮助。

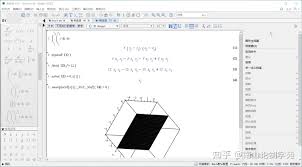
maple的微分命令以其简洁、准确、强大的特点，成为众多数学爱好者和专业人士的得力助手。它极大地简化了微分运算过程，让我们能够更专注于对数学问题的深入研究和探索。无论是学术研究还是实际应用场景，maple的微分功能都能为我们提供高效、准确的解决方案，难怪它如此受用户喜爱。