怎样用Maple做基础微分运算

maple是一款功能强大的数学软件，在基础微分运算方面表现出色。以下将详细介绍如何利用maple进行基础微分运算。

启动maple并输入函数

首先，启动maple软件。打开软件后，在输入提示符后输入你要进行微分运算的函数。例如，若要对函数$f(x)=x^2 + 3x + 1$进行微分，就在输入框中输入“f := x^2 + 3*x + 1;”，然后按下回车键，maple会将该函数定义为$f$。

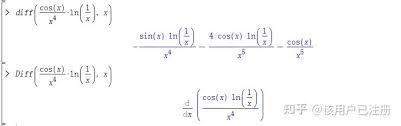
进行一阶微分

要计算函数$f$的一阶导数，只需输入“diff(f, x);”。这里的“diff”是maple中用于求导的命令，“f”是我们之前定义的函数，“x”表示对变量$x$求导。执行该命令后，maple会输出结果$2x + 3$，这就是函数$f(x)$的一阶导数。

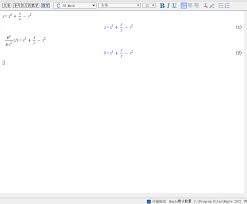
高阶导数计算

如果要计算高阶导数，比如函数$f$的二阶导数，输入“diff(f, x, x);”。maple会计算并输出结果$2$。若想求三阶导数，就输入“diff(f, x, x, x);”，以此类推，可根据需求计算任意阶导数。

多元函数微分

对于多元函数，例如$g(x,y)=x^2y + y^3$，定义函数“g := x^2*y + y^3;”。计算关于$x$的偏导数，输入“diff(g, x);”，得到$2xy$。计算关于$y$的偏导数，输入“diff(g, y);”，结果为$x^2 + 3y^2$。

隐函数微分

假设我们有隐函数方程$x^2 + y^2 = 25$。先将其定义为一个方程“eq := x^2 + y^2 = 25;”。然后使用隐函数求导命令“implicitdiff(eq, y, x);”，maple会输出$-x/y$，这就是隐函数$y$关于$x$的导数。

通过以上简单步骤，利用maple可以轻松完成各种基础微分运算。无论是一阶导数、高阶导数，还是多元函数的偏导数、隐函数的导数，maple都能快速准确地给出结果，大大提高了数学计算的效率和准确性，为数学学习和研究提供了有力的工具支持。