Mathematica与Maple哪个数论功能强

mathematica和maple作为两款强大的数学软件，在数论领域都有着出色的表现。

一、基本数论函数

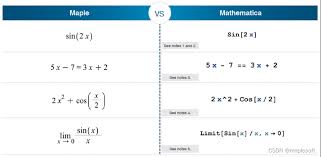
mathematica提供了诸如primeq判断素数、prime生成素数列表等丰富的基本数论函数。primeq[n]能快速准确判断n是否为素数，prime[n]则按顺序给出第n个素数。maple同样有isprime判断素数，ithprime生成指定位置素数的函数，在基本功能上与mathematica类似。

二、因数分解

mathematica的factorinteger函数能对整数进行因数分解，给出因数及其重数。例如factorinteger[12]可得到{{2, 2}, {3, 1}}。maple的ifactor函数也能实现整数因数分解，如ifactor(12)结果为2^2*3，二者在因数分解的功能上都较为强大且使用方便。

三、同余运算

mathematica通过mod函数实现同余运算，如mod[10, 3]可得到1。maple有modp函数，在同余计算上也能很好地完成任务，例如modp(10, 3)结果同样为1。

四、丢番图方程求解

对于简单的丢番图方程，二者都有一定的求解能力。mathematica可使用solve函数配合条件限定求解，如solve[x^2 + y^2 == 25, {x, y}, integers]可得到整数解。maple通过solve函数也能求解丢番图方程，如solve(x^2+y^2 = 25, {x, y}, integer)，不过在处理复杂方程时可能各有优劣。

五、性能与易用性

在性能方面，mathematica在大规模计算时速度可能稍快，尤其是涉及到复杂的数论算法。maple则在语法上可能对于初学者更易上手，函数命名直观。

mathematica和maple在数论功能上各有特色，都能满足数论研究和学习中的多种需求。用户可根据自身习惯和具体问题选择更适合的软件来助力数论问题的解决。